Marc Dupuis
Alcan International Limited
Arvida Research and Development Centre
1955 Mellon Blvd.
Jonquière, Québec, Canada G7S 4K8
The cathode of an aluminum reduction cell consists of a steel structure lined with bricks and other insulation materials. An efficient cell cathode design has an optimum heat balance that minimizes energy consumption and cell failure. The design relies on the solidification of the electrolyte against the side of the cathode to provide a "freeze" layer which protects the lining against erosion.
A three dimensional thermo-electric finite element ANSYS® model of a full quarter of the cathode was defined parametrically to allow for quick evaluation of design changes. For a given cathode design and cell amperage, the model calculates the steady state heat balance and freeze profile. For validation purposes, model results are compared against thermo-electric measurement campaigns (blitz).
INTRODUCTION
One of the mandates of the Electrolysis Technical Group is to develop analytical tools necessary to support major aluminium smelters. Advanced mathematical models are viewed as useful tools to help meet the environmental, technical and economic challenges that lie ahead.
This paper describes the use of the commercially available finite element program ANSYS to model the thermo-electric behavior of the aluminum reduction cells used at the Grande-Baie smelter.
Optimum Thermo-Electric Cell Design
Considerable electrical energy, around 14.5 kilowatt-hour per kilogram of aluminum for the Grande-Baie cell technology, is expended during the aluminum reduction process. Maintaining the proper heat balance in the cell is critical for minimizing energy consumption and promoting ease of cell operation. The design of the cell should be such that it maintains the correct operating temperature without excessive freeze coverage of the cathode blocks leading among other things to higher cell voltage, but with sufficient freeze to cover the side wall to prevent excessive side wall erosion and early side-lining failure.
Hence, thermo-electric optimization has the benefit of reducing both operating costs as well as the environmental impact of the process.
Imad Tabsh
Compusim Inc.
1003 D 55th Avenue N.E.
Calgary, Alberta, Canada T2E 6W1
The complex geometry and generation of heat within the cathode lining makes a combined calculation of the heat and current flow by finite element methods desirable. A thermo-electric model allows for the calculation of the location of isotherms in the lining, the freeze profile and the heat dissipated by the cathode. After validation of the model results against measurements obtained from thermo-electric "blitz" campaigns, the model can be used to investigate changes in the lining materials as well as changes in the process parameters.
Quarter Model Description
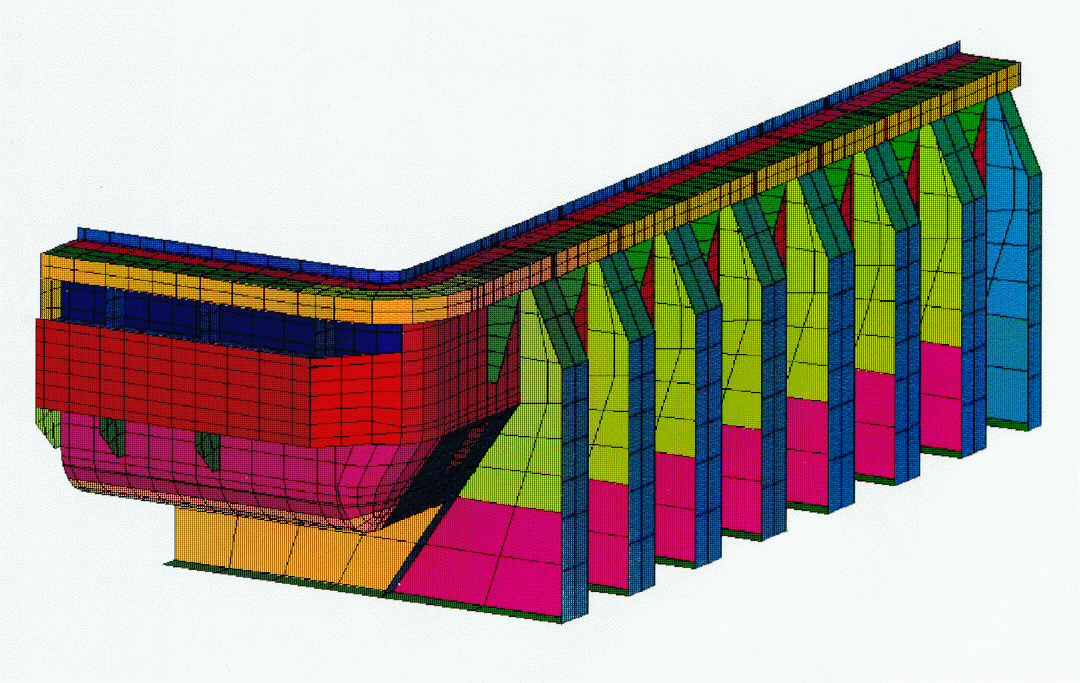
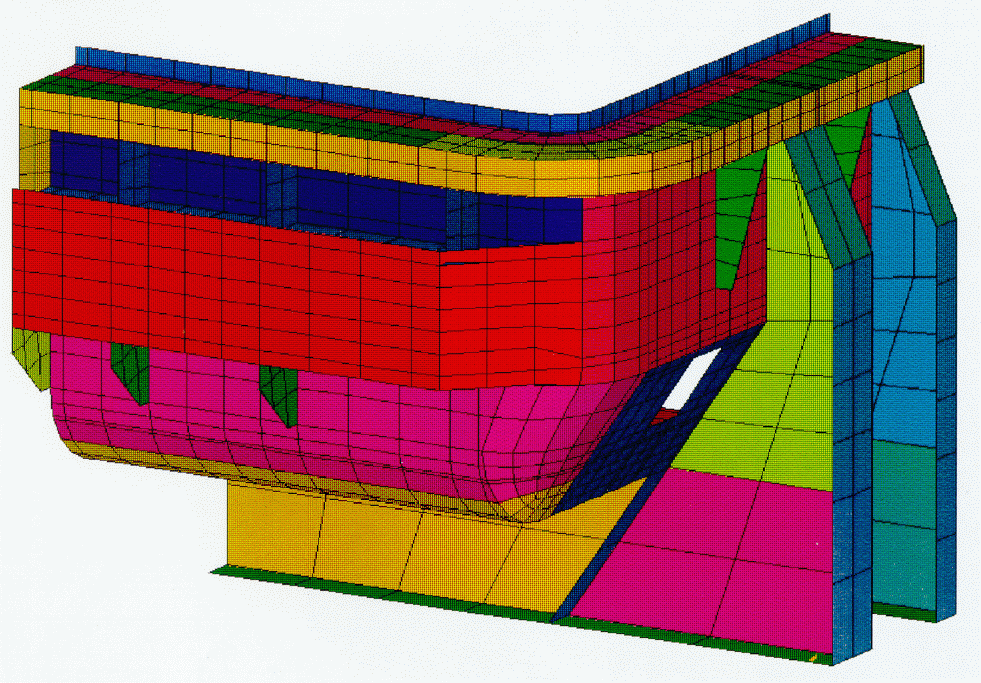
The cell technology used at the Grande-Baie smelter, with its sloped potshell side wall, its curved potshell end wall and its intricate pier design, has one of the more complex cathode lining geometries in the aluminum industry (Figure 1). The representation of such a complex geometry by a parametric finite element model proved to be quite an undertaking, especially in the corner zone between the side and end wall designs.

Figure 1: Grande-Baie Smelter Cathode Shell and Lining Design
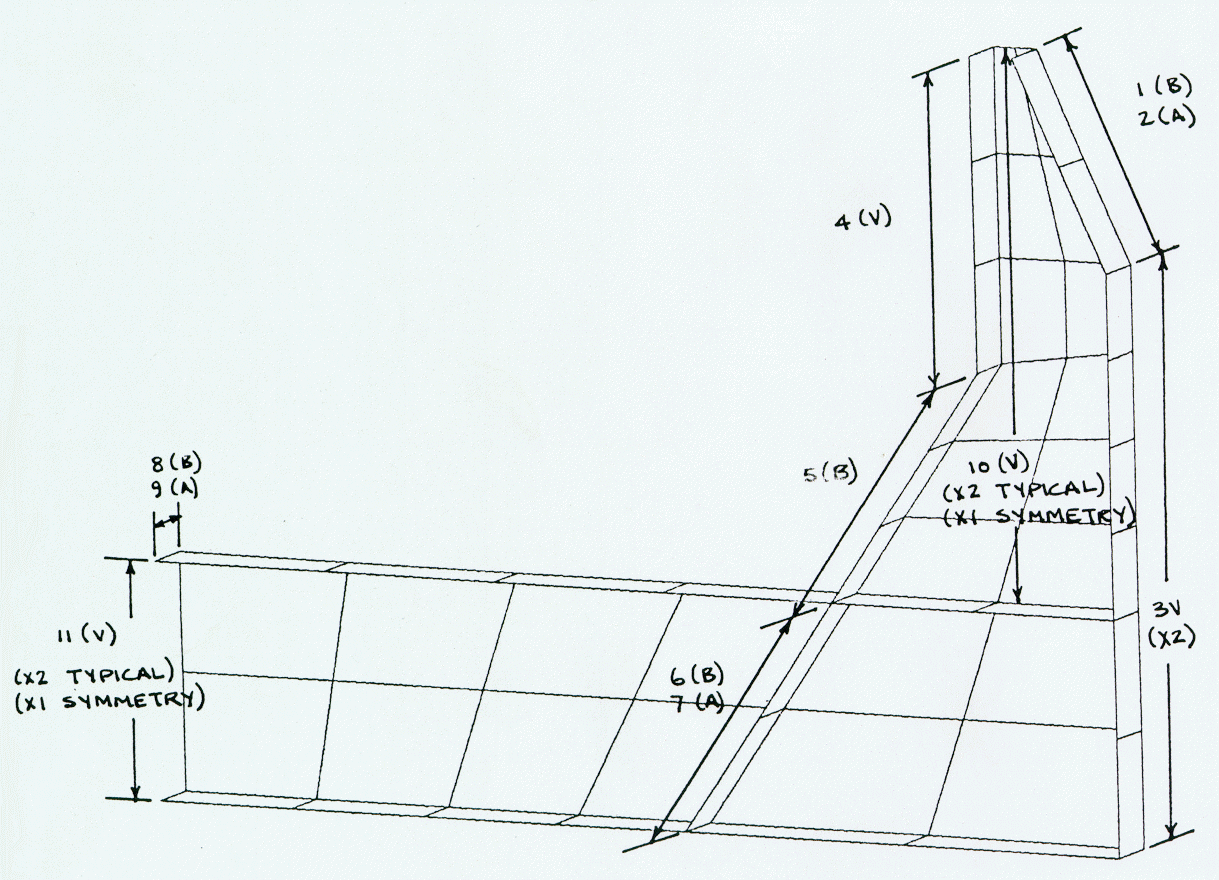
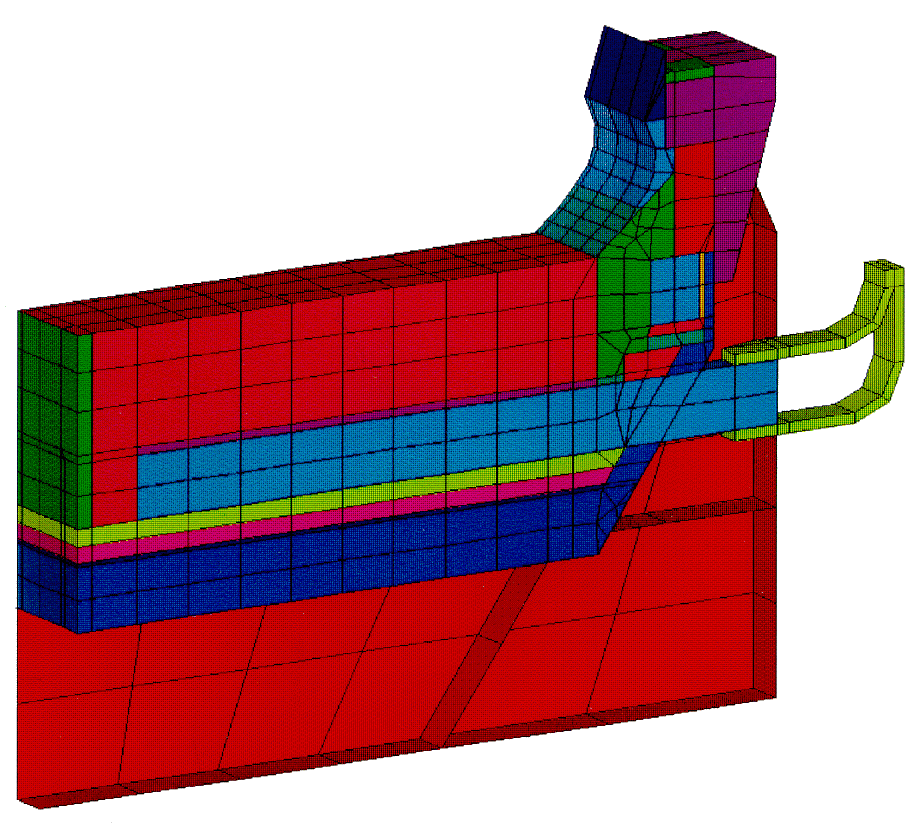
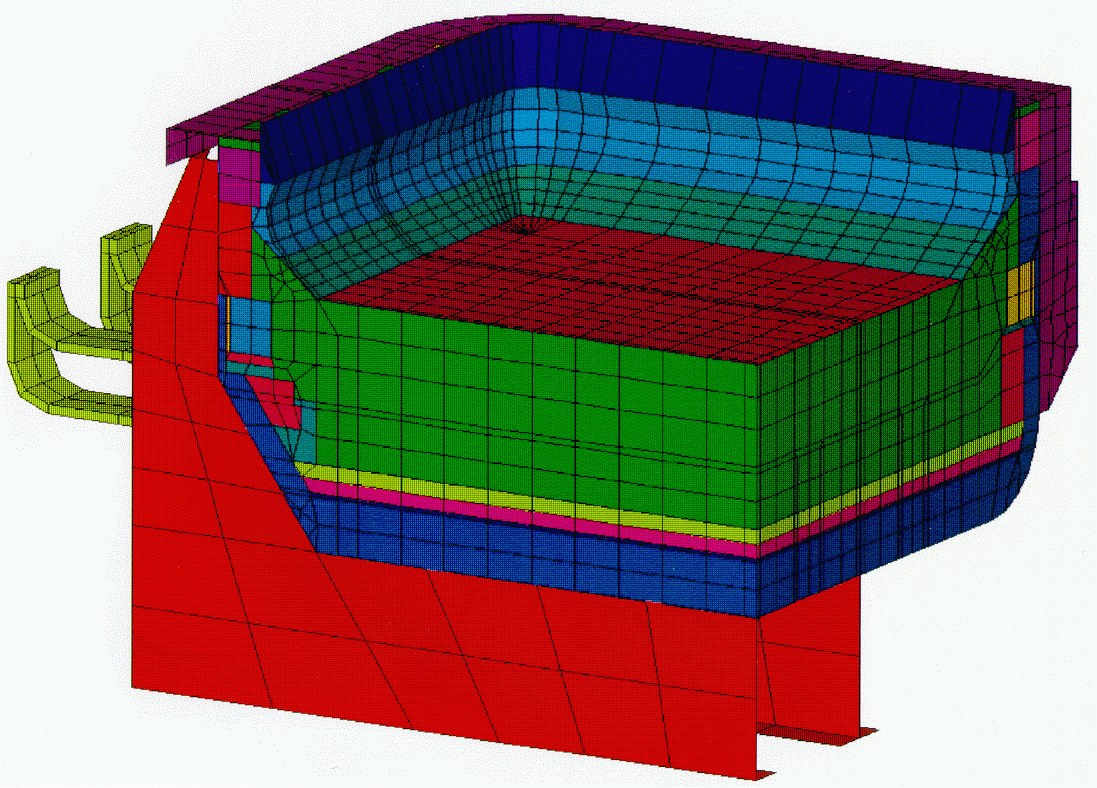
The geometric symmetry of the cell made it possible to model but a quarter of the cathode. The model consists of 21387 elements (Figure2). The geometry of the shell and lining was completely and uniquely represented by 109 independent size parameters Figure 3). Furthermore, 25 materials were used, each of which was defined with non-linear, temperature dependent properties. Heat loss to the environment by convection and radiation was represented using convection