Abstract
Finite element analysis (FEA) techniques are used extensively in industry to design new products and process vessels and to better understand the behavior of existing ones. This paper summarizes the authors' experience in using FEA to model Hall-Héroult reduction cells. FEA capabilities necessary to adequately simulate thermo-electric, electro-magnetic and stress fields within the cell are identified. Specific examples of models developed using the commercially available ANSYS® FEA program are discussed.
Introduction
The Hall-Héroult process is the only method used today for the industrial production of aluminum. Named after its inventors, Paul Héroult of France and Charles Hall of the USA, the process produces liquid aluminum by the electrolytic reduction of alumina dissolved into an electrolyte consisting primarily of cryolite.
The Hall-Héroult Reduction Cell
An aluminum reduction cell consists of a rectangular steel "open box" called a potshell supported by cradles and lined with refractory brick that surround the cathode carbon blocks. The lined potshell serves as the containment vessel for the electrolyte (also known as the bath) and the liquid metal being produced. A layer of frozen electrolyte (freeze) forms on the sides of the pot to protect the lining. Immersed in the bath are combustible carbon anodes suspended from a superstructure that is supported by the potshell. Figure 1 shows a schematic of a reduction cell.
Electric current is fed to the anodes via risers connected to an anode busbar. Within the cell, the current flows through the electrolyte to the metal pad and the cathode carbon and exits the cell via steel collector bars embedded in the cathode blocks. The collector bars are connected to the cathode busbars which in turn are connected to the risers of the adjacent pot. Typically, a smelter has one or more potlines each having 100-200 pots.
Design of An Optimum Reduction Cell
One of the main goals in designing a reduction cell is to reduce costs. Operating costs can be reduced by increasing pot life, reducing power consumption, improving metal quality and reducing man power requirements. Capital costs can be reduced by simplifying the cell design, reducing material requirements and reducing the building size to house the potline.
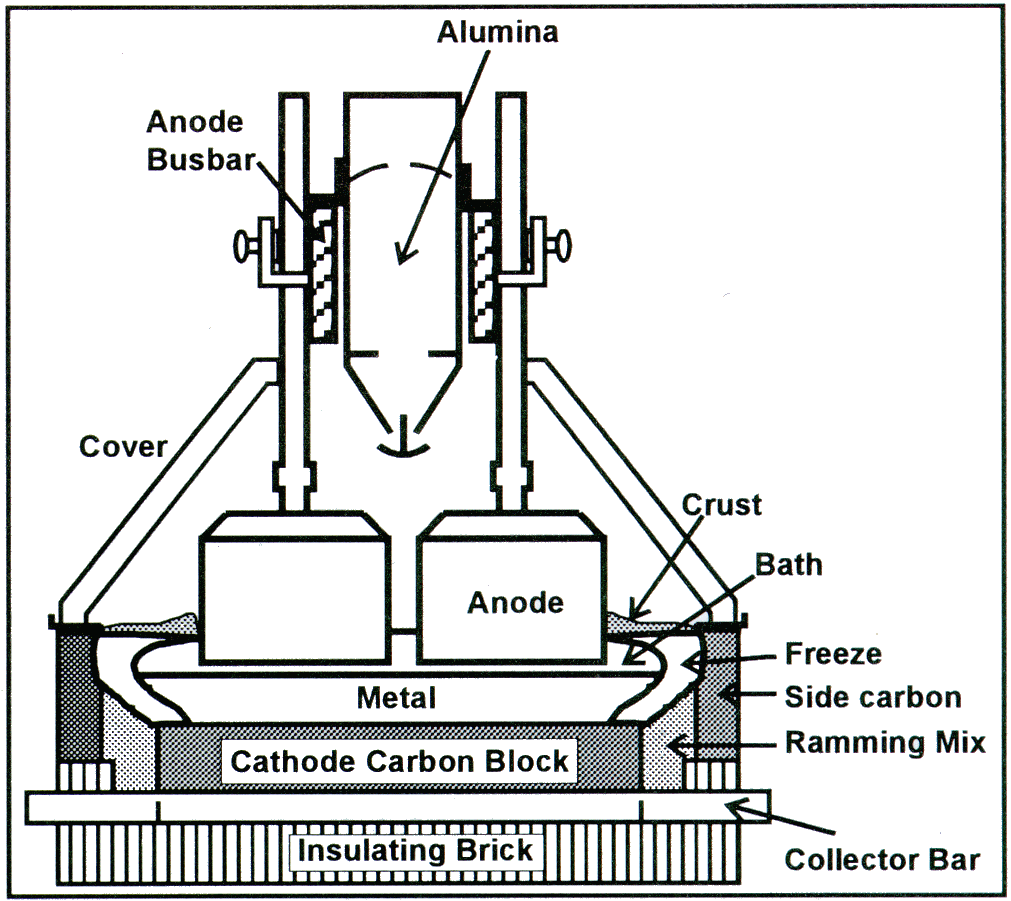
Figure 1: A schematic of an aluminum reduction cell
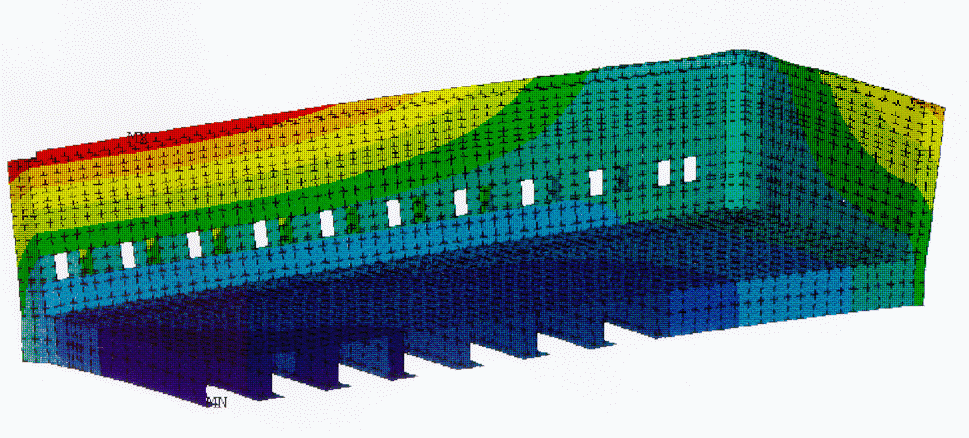
An optimal design of a cell requires a through understanding of the temperature and current distribution in the pot. The precise manner by which an aluminum reduction cell loses heat depends on the thermal insulation of the cell. This influences the formation of freeze which prevents early failure by erosion of the side wall. Power consumption is also affected by the thermal balance of the cell.
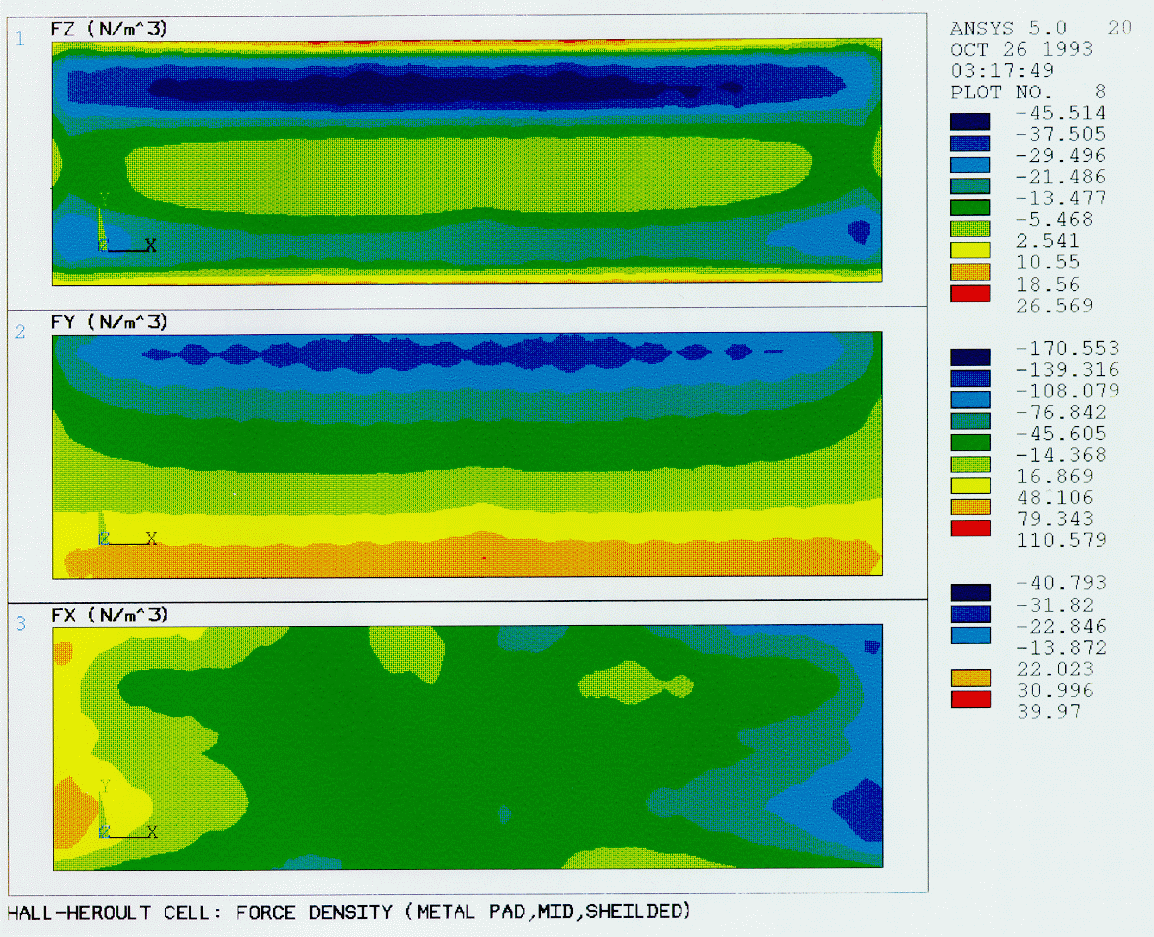
The current density distributions within the cell and in the surrounding busbar system generate strong magnetic fields which interact with the current distribution in the metal pad to produce Lorenz forces that induce motion of the metal. Stable operation of a cell requires a balanced busbar system and minimization of horizontal currents in the metal pad. The later are highly influenced by the shape of the freeze which in turn depends on the thermal balance of the cell.
The design of the cell is further complicated by the stresses generated in the carbon blocks and the potshell. These are due to the thermal gradients within the cell as well as the chemical loads due to the sodium diffusion into the cathode blocks and lining. The former can lead to distortion of the potshell that significantly alters the bath and metal height thus affecting the stable operation of the cell.