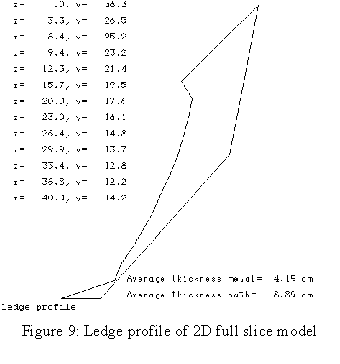This is why the next logical step was to produce 3D models[3]. Most of the time, the transition to 3D models also means the transition toward commercial software since the scope of developing a generic user-friendly FEM thermo-electric code exceeded the limited resources of «in-house» code developers.
The commercially available FEM code ANSYS® offered the required thermo-electric capabilities needed to build 3D thermo-electric models.
When the author joined the Alcan Research Center in Jonquière in 1984, he was given the mandate to develop a 3D half anode thermo-electric model using ANSYS®[5]. The next year, he developed a 3D cathode slice model followed by a 3D cathode corner model[6] which included an extra convergence loop to compute the position of the ledge profile[7]. The main drawback of those models was that they required enormous computer resources. As an example, the very first model built ran for two weeks elapsed time on a VAX 780!
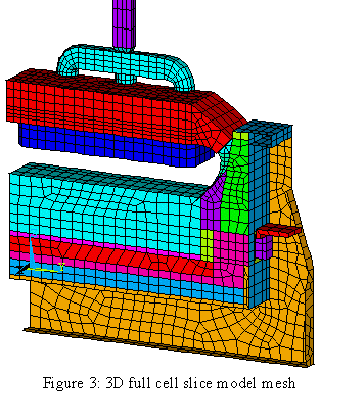
At the time, developing a complete 3D cell slice model that would have been the natural extension of existing 2D models was clearly not an option. Solving independently the anode and the cathode parts is a good modeling approach. The author expands on that in the next section of this paper and in his TMS industrial aluminum electrolysis course notes[1].
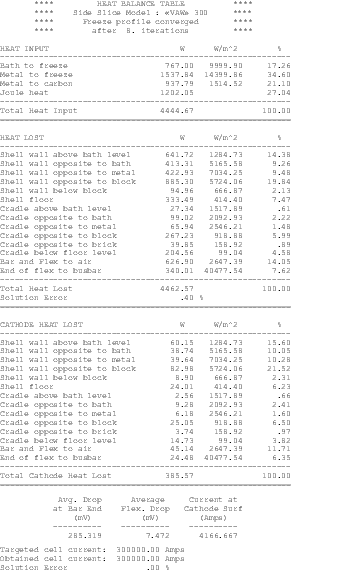
As computer resources started to become more available, it was possible to expand the 3D cathode slice model into a full quarter cell model[8,9]. At the same time, the extra ledge convergence loop that was initially developed to run on a VAX platform was recoded to be incorporated directly in ANSYS® by using the ANSYS® parametric design language (APDL) which means that the same model could be run on any computer platform.
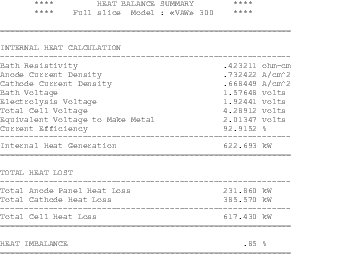
The availability of faster computers also permitted the development of 3D thermo-electric cell slice models[10,11]. It is now possible to develop full
thermo-electric corner/quarter cell model[12] and even coupled 3D magneto-hydrodynamic(MHD) and thermo-electric quarter cell model[13]. Unfortunately, the author thinks that the last two models mentioned still require too much computer resources to be consider as «practical» design tools today, maybe like the 3D half anode model was in 1984!
Considering the number of modeling options now available, the scope of this paper is to compare the relative merits of these 3D thermo-electric models to perform retrofit studies. The 2D model is also revisited to introduce a new improved approach.
3D thermo-electric half anode model
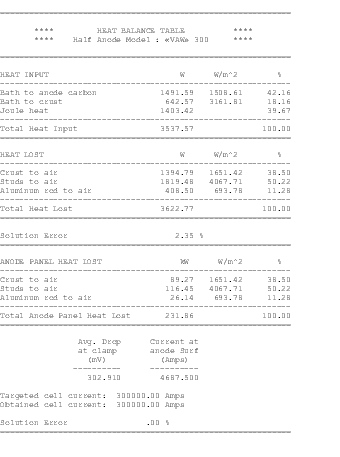
The 3D half anode model is quite efficient in the computation of the anode panel heat losses and the anode drop. The model takes advantage of the natural right/left symmetry that exists when the anode is away from the cell corner and the effect of the anode change pattern is neglected. The anode is modeled at mid-life with a typical layer of cover material (see Figure 1).
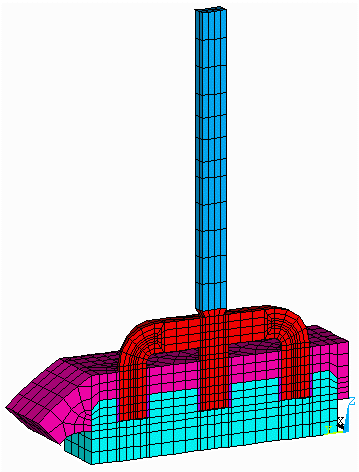
Figure 1: Half anode model mesh